Fließort von Schüttgütern

Der Fließort

Der Schertest simuliert die Umstände, denen ein Schüttgut typischerweise in Handlingsystemen ausgesetzt ist. Durch Spannungen, die auf ein Schüttgut einwirken, sind dessen Partikel zunächst einer elastischen, reversiblen Verformung ausgesetzt. Schüttgüter sind dabei in der Lage, auch ohne eine relative Bewegung der Partikel zueinander, Kräfte zu übertragen.

Überschreiten die Spannungen eine gewisse Grenzspannung, beginnen sich die Partikel relativ zueinander zu bewegen (plastische Verformung). Man nennt die Relativbewegung der Partikel auch scheren bzw. das Schüttgut fängt an zu fließen. Das Schüttgut wird dabei plastisch verformt. Wann ein Schüttgut beginnt zu fließen/scheren, hängt von den Einflussgrößen der Partikel zueinander und deren Packungszustand ab.

Der Widerstand, den ein Schüttgut dem Bruch in der Scherebene entgegensetzt, bevor es zu fließen beginnt, ist wesentlich von der Packungsdichte und somit von der Vorverdichtung (Konsolidierung) abhängig. Das Schüttgut ändert, abhängig von der Belastung und Bewegung, seine Packungsdichte und hat somit eine vom Spannungszustand abhängige Fließgrenze. Abgesehen von der elastischen Verformung, sind Schüttgüter dabei in der Lage, nach Wegnahme einer äußeren Belastung Packungszustände weitgehend beizubehalten.

Der Fließort beschreibt die Fließgrenze, also den Spannungszustand, bei dem das Schüttgut gerade im Begriff ist, sich auf der Gleitfläche unter Einwirkung der Schubspannung (τ) zu bewegen (fließen). Dabei führen größere Packungsdichten oft zu mehr Kontaktflächen zwischen den Partikeln und somit zu einem höheren Widerstand gegenüber beginnendem Fließen. Ein Schüttgut überträgt kleine Zugspannungen, überträgt ruhend Druck- und Schubspannungen und fließt unter der Einwirkung von Schubspannungen, wenn sie ausreichend groß sind.

Mit Schertestern lassen sich durch Messung des Fließortes die Beanspruchungen auf das Schüttgut definiert nachstellen und die resultierenden Fließeigenschaften messen. Dabei werden alle komplexen Einflussgrößen, welche die Fließfähigkeit beeinflussen, in ihrer Gesamtheit berücksichtigt. Man erhält qualitative reale Stoffdaten, die für weiterführende Berechnungen zum Einsatz kommen.

Normal- und Schubspannungen

Betrachtet man ein Volumenelement eines Schüttgutes, so wird eine an den Begrenzungsflächen (A) wirkende Kraft (F) aufgeteilt in eine

• Normalkraft (F_N), die senkrecht zur Fläche (A) wirkt
• und in eine Schubkraft (F_S), die rechtwinklig zur Normalkraft und parallel zur Fläche (A) wirkt.

Wie beim Druck, der das Verhältnis von Kraft zur Fläche beschreibt, spricht man in der Schüttgutmechanik von Spannungen, wenn man die Größe der einwirkenden Kraft relativ zur Begrenzungsfläche betrachtet. Relativ zur Fläche erhält man somit

• die Normalspannung (σ) (σ = F_N / A)
• und die Schubspannung (τ) (τ = F_S / A).

Insbesondere sind Schubspannungen für die Relativbewegung der Partikel zueinander, also für die plastische Verformung des Schüttgutes verantwortlich.

Horizontallastverhältnis

Wirkt eine Kraft auf ein Volumenelement eines Schüttguts, verteilt sich die Kraft je nach Materialeigenschaft räumlich unterschiedlich stark in verschiedene Richtungen. Dabei werden Kräfte (Spannungen) bei Schüttgütern über die Partikelkontakte, über Kraftlinien richtungsabhängig räumlich unterschiedlich stark übertragen. Daher stellt sich bei einer in vertikaler Richtung belasteten Druckspannung eine dem Schüttgut entsprechend kleinere Spannung in horizontaler Richtung ein. Das Verhältnis von Horizontaldruck (σ_h) zu Vertikaldruck (σ_v) wird als

Horizontallastverhältnis (λ = σ_h / σ_v)

definiert. Zu beachten ist, dass Druckspannungen in der Schüttgutmechanik im Gegensatz zur klassischen Mechanik als positive Spannungen definiert werden.

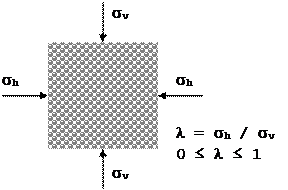
Bevor wir zum eigentlichen Schüttgut kommen, betrachten wir zunächst die beiden Grenzzustände, die theoretisch auftreten können:

(λ=1): In einer idealen Flüssigkeit treten keine Schubspannungen auf, da sich die Moleküle frei zueinander bewegen können und sich nicht, wie bei Schüttgütern, gegenseitig behindern. Diese Flüssigkeit ist inkompressibel, überträgt ruhend nur Druckspannungen und keine Zugspannungen. Der Druck in der Flüssigkeit breitet sich in gleicher Stärke räumlich aus. Das Verhältnis zwischen Horizontal- und Vertikaldruck ist λ=1.

(λ=0): Ein ideal steifer Festkörper überträgt Zug-, Druck- und Schubspannungen beliebiger Größe. Er deformiert unter den Einwirkungen reversibel (elastisch), fließt jedoch nicht. Das Horizontallastverhältnis λ=0.

(0<λ<1): Theoretisch kann sich ein Schüttgut im fluidisierten Zustand (die Partikel haben eine sehr lockere Packungsdichte) sowohl ähnlich einer Flüssigkeit als auch im anderen idealisierten Grenzfall wie ein Festkörper verhalten. Daher sind theoretisch im Schüttgut Spannungsverhältnisse zwischen Horizontalspannung (σ_h) und Vertikalspannung (σ_v) von 0<λ<1 möglich.

Betrachtet man nun dieses Volumenelement, welches an seinen Begrenzungsflächen als reibungsfrei angenommen wird, können dort keine Schubspannungen wirken. Die senkrecht zueinander stehenden auftretenden räumlichen Normalspannungen werden in diesen Ebenen zu

Hauptspannungen σ₁, σ₂ und σ₃.

Dabei ist definitionsgemäß die größte der drei Hauptspannungen σ₁, die kleinste σ₂ und die mittlere Hauptspannung σ₃.

σ₁ > σ₃ > σ₂

Für die Betrachtung in der Schüttguttechnik reichen in der Regel die größte und die kleinste Hauptspannung aus. Deshalb wird das Volumenelement so geschnitten, dass dessen Normale die mittlere Hauptspannung σ₃ ist und auf seinen Seiten jeweils die größte und kleinste Hauptspannung wirkt. Man spricht dann von einem ebenen Spannungszustand.

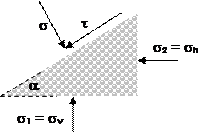
Wichtig in diesem Zusammenhang ist, dass wenn wir es mit Hauptspannungen zu tun haben, keine Schubspannungen auftreten. Im Inneren des Schüttgutelementes werden jedoch wohl Schub- und Normalspannungen in verschiedenen Lagen auftreten. Die Lage dieser Spannungen sind um den Winkel α in der Ebene gedreht.

Der Mohrsche Spannungskreis

Der mohrsche Spannungskreis ist ein von Christian Otto Mohr entwickeltes Verfahren zur grafischen Darstellung von Normal- (σ) und Schubspannungen (τ). Die Darstellung der Spannungen im mohrschen Spannungskreis ist das wichtigste Hilfsmittel zur Veranschaulichung und Auswertung in der Schüttgutmechanik. Er dient als geometrische Darstellung der Gleichgewichtsbedingungen und veranschaulicht die Spannungen in beliebigen Schnittebenen.

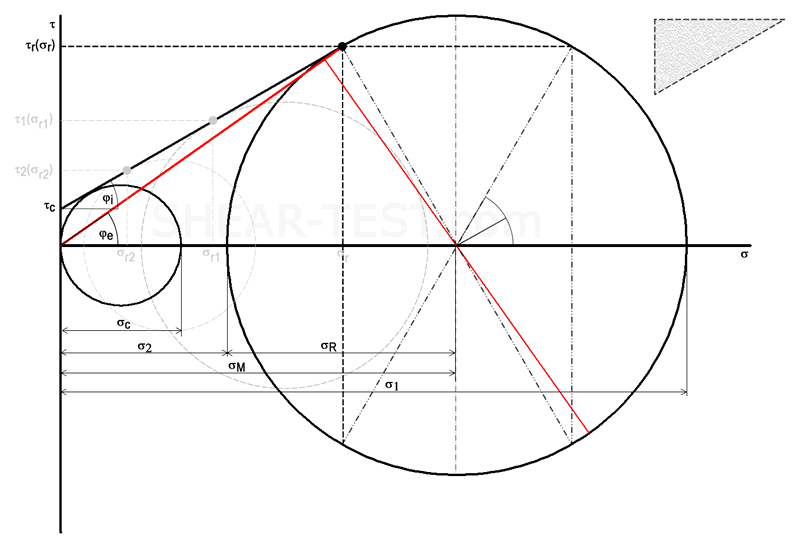
Durch Wahl der richtigen Schnittebene erhält man den ebenen Spannungszustand, der die Lage der größten und kleinsten Hauptspannung richtig beschreibt. In diesem ebenen Spannungszustand gibt es stets zwei senkrecht zueinander verlaufende Hauptspannungen (σ₁ und σ₂), für die die Normalspannungen extrem werden, während gleichzeitig die Schubspannungen verschwinden. Der resultierende mohrsche Spannungskreis bildet zwei Schnittpunkte mit der σ-Achse, wodurch dieser durch die Lage der Hauptspannungen σ₁ und σ₂ vollständig beschrieben wird.

Geht man davon aus, dass keine Schubspannungen auf ein Schüttgutelement einwirken, aber sehr wohl Druckspannungen in den Hauptspannungsebenen, stellt sich über das Horizontallastverhältnis (λ) die kleinere Hauptspannung σ₂ ein. Durch Erhöhung der Hauptverfestigungsspannung (σ₁) (die dadurch nach rechts verschoben wird) werden sich immer größere Radien des mohrschen Spannungskreises einstellen und auch σ₂ wird seine Position auf der σ-Achse über das Horizontallastverhältnis entsprechend verändern.

In dem Punkt, der den Spannungskreis tangiert, herrschen die Bruchspannungen (σ,τ) in der Gleitfläche, die mit der Ebene der Hauptspannungen den Winkel α bildet. Damit ist die Lage der Gleitfläche durch den Winkel der inneren Reibung (φ_i) bestimmt. Jede (σ,τ) Kombination, die auf der coulombschen Geraden liegt, führt zum Fließen des Schüttgutes. Spannungszustände unterhalb der Geraden sind stabil, solche oberhalb sind physikalisch nicht möglich.

Die größte Hauptverfestigungsspannung (σ₁) bewirkt die Schüttgutverfestigung auf die entsprechende Porosität und wird deshalb auch als Verfestigungsspannung bezeichnet und dient daher auch als Basis für Funktionen der Stoffdaten.

Wird ein weiterer Mohrkreis mit der kleinsten Hauptspannung σ = 0 konstruiert, der den Fließort ebenfalls tangiert, so resultiert bei der größten Hauptspannung die Druckfestigkeit (σ_c) des Schüttgutes. Das Verhältnis von Druckfestigkeit zur größten Hauptspannung wird gerne zur Klassifizierung der Fließfähigkeit eines Schüttgutes herangezogen. Die Druckfestigkeit ist ebenfalls wichtig für die Bestimmung von Brückenbildung in einem Silo.

Messungen des Fließortes mit Schertestern

Schertester werden in der Bodenmechanik als Standarduntersuchungsmethode zur Bestimmung der Scherfestigkeit von Böden verwendet. A. W. Jenike übertrug diese physikalischen Grundlagen auf die Schüttgüter der Verfahrenstechnik und leitete davon Stoffgrößen ab, die eine Konstruktion von Silos mit ungestörtem Ausfließen ermöglichen sollten. Seit die aus dem Schertest abgeleiteten Parameter zur Dimensionierung verwendet werden, ist es möglich, das verfahrenstechnisch relevante Verhalten der Schüttgüter vorherzusagen.

Beim Schertest wird bei einem definierten Konsolidierungszustand, also bei einer definierten Packungsdichte, die Scherspannung bei verschiedenen Normalspannungen bestimmt. Die σ-τ-Messwerte ergeben den Fließort (YL) unter den zuvor eingestellten Bedingungen. Für jede Ausgangsdichte existiert ein entsprechender Fließort.

Zur Messung eines Fließortes wird eine Probe auf eine der Anwendung entsprechende Packungsdichte konsolidiert, um sie anschließend bei einer niedrigeren Normalspannung (σ) abzuscheren. Dabei wird die jeweilige Schubspannung (τ) gemessen. Wiederholt man dieses mit der jeweils gleichen Ausgangsdichte aber unterschiedlichen Abscherspannungen, erhält man die Lage des Fließortes. Diese Fließgrenze beschreibt den Spannungszustand, bei dem das Schüttgut gerade im Begriff ist, sich auf der Gleitfläche unter Einwirkung der Schubspannung zu bewegen (fließen). Mehrere Fließorte, abgeleitet von verschiedenen Ausgangsdichten, werden als Fließortschar bezeichnet.

Durch die Messungen und Auswertung erhalten wir so grundlegende physikalische Stoffdaten, die zur Charakterisierung und Unterscheidung von Schüttgütern und für weitere technologische Berechnungen herangezogen werden können.

Wichtige Kennwerte:

• innerer Reibungswinkel (φ_i),
• effektiver Reibungswinkel (φ_e) mit dem das Horizontallastverhältnis (λ bzw. K) zwischen Horizontal- und Vertikaldruck hergeleitet werden kann,
• Kohäsion (τ_c),
• die Druckfestigkeit (σ_c),
• Fließfähigkeitsfaktor (FL bzw. ffc),
• Schüttgutdichte nach der Konsolidierung im ruhenden Zustand und Fließzustand.

file name

YL-150-a.yl

date

05 May 2016

material

validation powder

client

SHEAR-TEST.com

operator

MB

humidity

12.47 % Moisture

note

device

ST200AUTO

shear cell

RSL-ST30.cel

Δσ

+ 0 Pa

ΔΤ

+ 0 Pa

ρb0 =

0.479

g/cm³

bulk density

ρbr =

0.702

g/cm³

density σr

use prorating

YIELD LOCUS EVALUATION RESULTS

φe =

34.6

deg

effective angle of friction (≙ Φi at EN1991-4) ⇒ K

φi =

30.9

deg

angle of internal friction (≙ Φc at EN1991-4), (DEM := static friction)

Τc =

755

Pa

cohesion (≙ c at EN1991-4), (DEM := cohesion)

σ1 =

30941

Pa

major principal stress

σ2 =

8560

Pa

minor principal stress

σc =

3045

Pa

unconfined compressive strength

σt =

-747

Pa

tensile strength

...

FL =

10.16

flowability factor = σ1 / σc

R =

0.999

coefficient of correlation

...

Effektiver Reibungswinkel

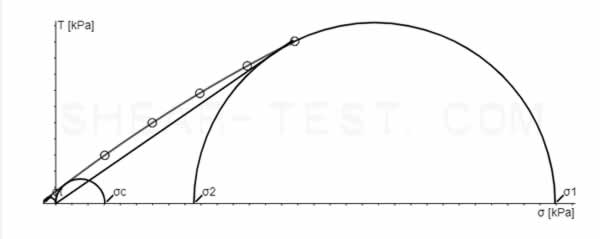
Wichtig ist, dass die Lage des Fließortes von der Packungsdichte/Konsolidierung abhängig ist. Für jede Ausgangsdichte existiert ein entsprechender Fließort. Er liegt umso höher, je dichter die Probe gepackt ist. Da man im Vorfeld nicht genau weiß, welcher Spannungszustand im Anwendungsfall genau auftritt, werden mehrere Fließorte mit unterschiedlichen Referenzspannungen (σ_r) gemessen, um anschließend die Ergebnisse interpolieren zu können.

Der effektive Reibungswinkel (φ_e) bildet dabei eine Funktion, welche die jeweils großen Mohrschen Spannungskreise tangiert. Mithilfe des effektiven Reibungswinkels kann dann für jeden beliebigen Spannungszustand zwischen den gemessenen Fließorten das Horizontallastverhältnis (λ) = (Horizontaldruck (σ_h) / Vertikaldruck (σ_v)) hergeleitet werden.

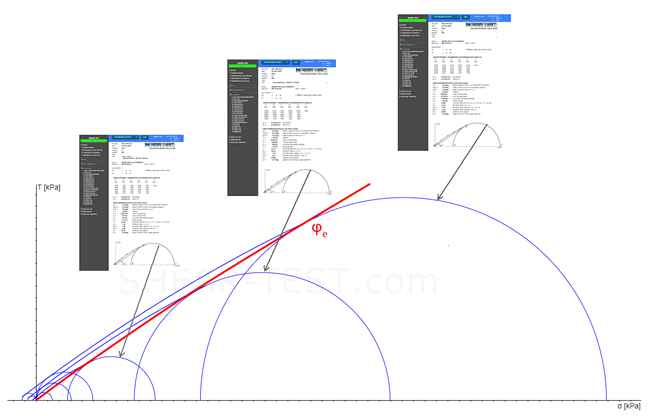
Drei Fließorte (blau) des gleichen Materials bei unterschiedlichen Referenzspannungen (σ_r)
effektiver Fließort (rot)

Berechnung der Spannungszustände zwischen den gemessenen Fließorten

Hauptspannungen berechnet vom effektiven Reibungswinkel σ₁(φ_e), σ₂(φ_e)
Druckfestigkeit berechnet durch Fließfunktion σ_d(σ₁)